| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- hackerrank
- 스파르타
- 실전 데이터 분석 프로젝트
- 파이썬 머신러닝 완벽 가이드
- 내일배움카드
- 중회귀모형
- 티스토리챌린지
- wil
- 미세먼지
- Cluster
- 회귀분석
- MySQL
- R
- TiL
- 파이썬 철저 입문
- 파이썬 철저입문
- 스파르타코딩
- 웹 스크랩핑
- 텍스트 분석
- 파이썬
- 파이썬 완벽 가이드
- SQL
- 파이썬 머신러닝 완벽가이드
- harkerrank
- 오블완
- 내일배움캠프
- 내일배움
- 스파르타 코딩
- 프로그래머스
- 프로젝트
- Today
- Total
OkBublewrap
[통계 101 x 데이터 분석] 모형 본문
모형이란?
통계 모형, 기계학습 모형, 수리 모형
이와 함께 또 하나의 중요한 모형으로 수리 모형이 있습니다.
수리 모형은 현상의 프로세스나 메커니즘을 가정하고 그 움직임을 조사하는 모형
수리 모형은 메커니즘을 수학적으로 나타내는 것에서 출발하여 논리적으로 무엇이 일어나는가를 조사하는 방법입니다.
그러므로 연역적인 방법입니다.
많은 경우 메커니즘에 기반을 둔 모형을 구축하기 때문에,
데이터로 경험하지 못한 범위라도 예측이나 통제가 가능할 때가 있습니다.

모형은 현상을 이해하는 도구
모형이란, 현상을 잘 기술하여 이해할 수 있도록 간략화하는 방법이다.
모형을 만들 때는 현상의 본질을 유지하면서 간략화하는 방법입니다.
모형화란 간략화를 통해 사물의 본질을 이끌어 내는 일인 것 같습니다.
완벽한 모형은 없다
현상의 실제 모습 = 실제 모형을
만들기란 불가능하다고 할 수 있습니다.
모형은 어디까지나 현상을 이해하는 데 도움이 되는 근사 도구로,
실제 현상 그 자체와 모형은 다르다는 사실을 명심하는 것이 중요합니다.
수리 모형이란?
가상의 세계를 상정하고 어떤 규칙을 적용했을 때
일어나는가를 조사하는 방법입니다.
수리모형 종류
- 결정론 모형 : 미분 방정식, 차분 방정식, 편미분 방정식
- 확률 모형 : 무작위 행보, 마르코프 연쇄
결정론이란, 특정 시각의 상태가 정해지면 다음 시각의 상태는 단 하나로 정해지는 성질을 말합니다.
즉, 확률적인 성질이 없다.
운동방정식은 특정 방향, 특정 속도로 공을 던졌다면 어디에 떨어질지를 반드시 예측할 수 있으므로 결정론이다.
결정론적인 성질이 현상의 본질일 떄는 결정 모형을 사용하면 좋습니다.
도박에서 이기거나 지는 것을 반복할 때는 확률적인 변동이 중요한 요소가 됩니다.
이러한 현상에는 확률 모형을 적용할 수 있습니다.
수리 모형 분석하기
모형의 복잡함과 이해의 용이함 간에는 상충 관계가 있다
수리 모형 : 미분 방정식
미분 방정식과 차분 방정식
대표적인 수리 모형으로 결정론 모형인 미분 방정식(차분 방정식)이 있다.
미분 방정식을 포함한 수리 모형의 목적은 주어진 규칙에 따랐을 때 무엇이 일어나는가를 조사하는 것
특히, 미분 방정식은 시간과 함께 변수 X가 어떻게 변하는가와 같은 시계열 움직(동역학)을 대상으로 합니다.
수리 모형 사례 1 : 수의 변화를 모형으로
밤과자가 2배씩 늘어나는 현상을 모형으로 나타내기
$$ x_{t+1} = 2x_{t} $$
이는 증가 규칙을 나타낸 차분 방정식 입니다. 이 규칙을 따를 때 어떤 일이 생길까
또 하나의 방법은 이 차분 방정식을 푸는 것이다.
$$ x_{t} = 2^{t} $$
지정한 시각 t의 $ x_{t} $를 알 수 있음
지수함수이므로 지수함수 증가(또는 지수 증가)라 합니다.

다른 현상임에도 같은 수식으로 모형화할 수 있는 것은,
증가하는 양이 현재 수에 따라 달라지는 성질이 공통적이기 때문이다
이 모형은 그 본질을 잘 포착하고 있는 것입니다.
지수 증식의 일반해와 분기 다이어그램
파라미터 r에 따라 증가 방식이 변화
차분 방정식
$ x_{t+1} = rx_{t} $
↓
$ x_{t} = x_{0}r^{t} $


r = 1을 경계로 질적인 움직이 변화
r > 1 지수적으로 증가
r < 1 지수적으로 감소(0까지)
이처럼 파라미터를 다양하게 바꾸었을 때 어떤 일이 일어나는가를 조사할 수 있다는 것이 수리 모형의 강점입니다.
미분 방정식
차분 방정식에서는 시간 t가 0, 1, 2.. 와 같이 이산적인 값이었는데. 이산적인 값이었는데,
이 시간 간격을 작게 하면 연속 시간 모형인 다음 식을 얻을 수 있습니다.
$$ \frac{dx}{dt} = ax $$
이것이 미분 방정식(differential equation)으로, 아주 짧은 시간의 변화율을 나타냅니다.
가장 단순한 선형 미분 방정식으로, 다음과 같이 간단하게 해를 얻을 수 있습니다.
$$ x(t) = x(0)e^{at} $$
지수적 증가 또는 감소라는 성질은 같으나 그 경계가 파리머 a=0이 됩니다.
왜냐하면 미분 방정식은 변화율을 표시하므로, 0보다 크면 증가, 0보다 작으면 감소를 나타내기 때문입니다.
밀도효과
x가 늘어날수록 그 증가율이 줄어드는 효과, 즉 밀도 효과를 적용한 모형을 생각하는 것이 자연스럽다.
흔히 사용되는 것이, 다음과 같은 형태의 로지스틱 방정식입니다.
$$ \frac{dx}{dt} = ax\left [ 1 - \frac{x}{K} \right ] $$

로지스틱 방정식에서는 시간이 흐를수록 K라는 값으로 포화한다는 것을 알 수 있습니다.
그리고 일단 x=K가 되면 증가하지도 감소하지도 않는 상태가 됩니다. 이를 평형 상태 또는 평형점이라 합니다.
x가 K보다 작거나, 커지더라도 x=K인 평균 상태로 되돌아가는 성질이 있습니다. 이러한 평형점을 안정평형점이라 부릅니다.
x가 K보다 크면 dx/dt<0이 되어 x가 줄어들고, x가 K보다 작으면 dx/dt>0이 되므로 x는 늘어나기 때문입니다. 반면 x=0인 평형점에서는 x가 0보다 조금이라도 커지면 dx/dt>0이 되어 x는 늘어나기 시작합니다. 일단 x=0을 벗어나면 자연적으로 이 평형점으로 되돌아가는 일은 없기 때문에, 불안정평형점이라 합니다.
이처럼 세운 미분 방정식의 평형점을 조사하고, 그 평형점이 안정인지 불안정인지를 확인함으로써,
그 모형의 성질 일부를 밝힐 수 있습니다.
선형과 비선형
미분 방정식은 선형과 비선형으로 분류할 수 있습니다.
선형 방정식이란 변수 x의 정수배와 총합으로 작성할 수 있는 방정식을 가리킵니다.
선형과 비선형의 차이를 직관적으로 이해하기 위해서는,
선형은 항상 규칙이 같은 데 비해 비선형은 변수 x의 값에 따라 규칙이 달라진다는 생각을 하면 좋다.
수리 모형 사례 2 : 감염병 모형
이번에는 3개의 변수 S(t)(감수성 보유자, Susceptible), I(t)(감염자, Infected), R(t)(회복자, Recovered)가 있고, 시각 t에서 각각의 사람 수를 나타냅니다.
S(t) + I(t) + R(t) = 사람 수로, 전체 사람 수는 달라지지 않는닥 가정하면, 인구를 1로 하여 S(t), I(t), R(t)를 비율로 해석할 수 있습니다. 감수성 보유자는 감염자와 접촉하면 일정 감열률로 감염자로 변하고(즉, 감염), 감염자는 일정 비율로 회복자로 변합니다
$$ \frac{dS}{dt} = - \beta S(t)I(t) $$
$$ \frac{dI}{dt} = \beta S(t)I(t) - \gamma I(t) $$
$$ \frac{dR}{dt} = -\gamma I(t) $$
이것이 감염병의 기본 모형으로, SIR 모형이라 불립니다. S와 I가 곱해지는 까닭은, 감염에 대한 감수성이 감염자의 수에 비례하기 때문입니다. 이 항이 있으므로 SIR 모형은 비선형인 미분 방정식이 된다.
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp
# SIR 모델 방정식 정의
def sir_model(t, y, beta, gamma):
S, I, R = y
dSdt = -beta * S * I
dIdt = beta * S * I - gamma * I
dRdt = gamma * I
return [dSdt, dIdt, dRdt]
# 초기 조건 설정
N = 1000 # 총 인구
I0 = 1 # 초기 감염자 수
S0 = N - I0 # 초기 감염되지 않은 인구
R0 = 0 # 초기 회복자 수
beta = 0.3 # 감염률 (전파 속도)
gamma = 0.1 # 회복률 (1/평균 감염 기간)
# 시간 설정
t_span = (0, 160) # 시뮬레이션 기간 (0일부터 160일)
t_eval = np.linspace(0, 160, 1000) # 1000개 점으로 시간 분할
# 미분방정식 풀기 (ODE solver 사용)
sol = solve_ivp(sir_model, t_span, [S0/N, I0/N, R0/N], args=(beta, gamma), t_eval=t_eval)
# 결과 데이터 저장
S, I, R = sol.y
# 그래프 그리기
plt.figure(figsize=(10, 6))
plt.plot(sol.t, S, label="Susceptible", color="blue")
plt.plot(sol.t, I, label="Infected", color="red")
plt.plot(sol.t, R, label="Recovered", color="green")
plt.xlabel("Days")
plt.ylabel("Fraction of Population")
plt.title("SIR Model Simulation")
plt.legend()
plt.grid()
plt.show()
S와 I가 곱해지는 까닭은, 감염에 대한 감수성이 감염자의 수에 비례하기 때문이다.
이 항이 있으므로 SIR 모형은 비선형인 미분 방정식이 됩니다.
S(0) = 0.999, I(0) = 0.001, R(0) = 0으로, 감염자가 없는 상태에서 아주 약간의 감염자가 발생했음을 나타냅니다.
감염 초기에는 감염자가 지수적으로 증가하여 감염이 급속히 확산되는 것을 알 수 있습니다. 그러다 감수성 보유자(S)가 줄어들면서 감염자 수도 줄기 시작하고, 마지막에는 많은 사람이 감염을 경험한 회복자(R)가 됩니다.
분기 다이어그램
$$ \frac{dI(0)}{dt} = \beta S(0)I(0)-\gamma I(0) = I(0)(\beta S(0)-\gamma ) >0 $$
기초감염재상산수 $ R_{0} $를 다음과 같이 정의하여 조건을 다시 쓰면 다음과 같습니다.
$$ R_{0} = \frac{\beta }{\gamma }S(0) > 1 $$
S(0)은 거의 1이므로, 베타 / 감마가 1보다 큰지가 유행 진입 여부를 결정합니다.
R0은 기초감염재생산수로 1보다 크다면 유행이 확산된다는 것을 직관적으로도 알 수 있다.
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import fsolve
# 최종 감염되지 않은 비율 S_inf 계산 함수
def final_susceptible(S_inf, R0):
return S_inf - np.exp(-R0 * (1 - S_inf))
# R0 범위 설정
R0_values = np.linspace(0.5, 3, 100)
R_inf_values = []
# 각 R0에 대해 R_inf 계산
for R0 in R0_values:
S_inf_guess = 1 if R0 < 1 else 0.5 # 초기 추정값
S_inf_solution = fsolve(final_susceptible, S_inf_guess, args=(R0))
R_inf = 1 - S_inf_solution[0]
R_inf_values.append(R_inf)
# 그래프 그리기
plt.figure(figsize=(8, 5))
plt.plot(R0_values, R_inf_values, label='최종 R', color='blue')
plt.axvline(x=1, color='black', linestyle='--', linewidth=2, label=r'$R_0 = 1$ (Threshold)')
# 추가적인 설명 라벨
plt.text(1 - 0.02, 0.5, "유행X", fontsize=12, color="black", horizontalalignment='right')
plt.text(1 + 0.02, 0.5, "유행O", fontsize=12, color="black", horizontalalignment='left')
plt.xlabel('베타 / 감마')
plt.ylabel('최종 R')
plt.title("SIR 모형의 분기 다이어그램")
plt.legend()
plt.grid(True)
plt.show()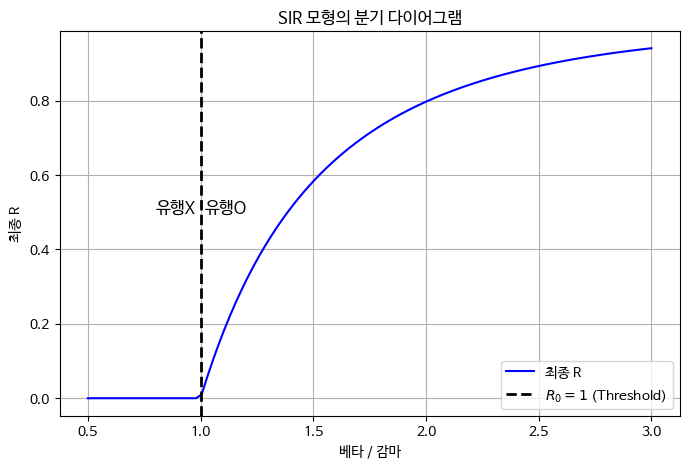
가로축이 기초감염재상산수, 세로축이 최종 회복자 수 R(기감염자 수)인 그래프입니다. 비율 = 1을
경계로 유행 시작 여부가 판가름 난다는 것을 알 수 있습니다.
감마가 달라진 경우에는 실질감염재생산수 R를 생각할 수 있습니다.
마스크를 쓰거나 외출을 자제하는 등의 행동 변화는 원래의 베타를 작게하는 변화에 해당하고,
감염되었을 때 조기에 격리하는 대칙은 감마를 크게 하는 변화에 해당된다.
접촉률이 반이 되면 베타도 반으로 줄어들고, 실질감염 재생산수 R는 원래 기초감염재생산수 R의 반으로 줄어듭니다.
이에 따라 예를 들어 R=1.8로 확산될 터였던 유행을 억제하는 일이 가능합니다.
SIR 모형의 결과가 우리가 감염병 예방에 있어 중요하다고 여겼던 것들을 분명히 나타내고 있으므로, 감염병 유행이라는 현상에 대해 한층 깊에 이해할 수 있다.
예측
지금까지 수리 모형을 구축하고, 파라미터를 바꿔 가면서 이를 통해 현상을 이해하고자 했다.
데이터로 모형의 파라미터를 추정하면 미래의 값을 예측할 수 도 있습니다.
단, 지금까지의 파라미터(감염 규칙)가 달라지지 않는다는 것을 전제로 한 예측이라는 점을 주의 해야한다.
통제
더 나아가 일단 수리 모형을 만들어 두면, 만약 ~이라면 어떤 일이 일어날까, 어떻게 하면 바라는 상태를 만들 수 있을까 등의 문제를 모형상에서 생각할 수 있습니다.
계속해서 감염병 수리 모형을 예로 들겠습니다. 감염이 널리 퍼진 후, 면역 보유자가 있는 상황에서 1명의 감염자가 감염시킬 신규 감염자 수인 실질감염 재생산수 R(t)를 줄일 수 있었다면, 감염자 수가 어떤 변화를 보일 것인가를 다양하게 시뮬레이션할 수 있습니다. 거꾸로 이야기하면 전염병을 감소시키고자 한다면 실질감염재생산수 R(t)를 어느 정도로 작게 해야 좋을지도 알 수 있습니다.
이처럼 수리 모형을 이용하여 시나리오를 탐색하는 접근법은 경험하지 못한 것, 즉 데이터로 얻을 수 없는 조건에 관해서도 지식을 얻는 방법으로, 통계 모형이나 기계학습 모형에는 없는 강점이다.
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
# SIR 모델 방정식 정의
def sir_model(y, t, beta_func, gamma):
S, I, R = y
beta = beta_func(t) # 시간에 따라 beta 변경
dSdt = -beta * S * I
dIdt = beta * S * I - gamma * I
dRdt = gamma * I
return [dSdt, dIdt, dRdt]
# 초기 조건 및 파라미터 설정
N = 1000 # 총 인구 수
I0, R0 = 1, 0 # 초기 감염자 및 회복자 수
S0 = N - I0 - R0 # 초기 감수성 인구
gamma = 0.1 # 회복률
# R_t 값에 따른 beta 변화
Rt_values = [1.5, 1.2, 0.8, 0.6]
beta_values = [rt * gamma for rt in Rt_values]
def beta_func_factory(beta_before, beta_after):
def beta_func(t):
return beta_before if t < 20 else beta_after
return beta_func
# 시간 범위 설정
t = np.linspace(0, 50, 200)
# 초기 예측 모델 (t=50까지 감염 예측)
beta_initial = 0.3
def beta_initial_func(t):
return beta_initial
initial_solution = odeint(sir_model, [S0/N, I0/N, R0/N], t, args=(beta_initial_func, gamma))
# 여러 R_t 값에 대한 SIR 모델 계산
solutions = []
for beta_after in beta_values:
beta_func = beta_func_factory(0.3, beta_after)
solution = odeint(sir_model, [S0/N, I0/N, R0/N], t, args=(beta_func, gamma))
solutions.append(solution)
# 시각화
plt.figure(figsize=(10, 6))
# 첫 번째 그래프 (예측값 포함)
plt.subplot(1, 2, 1)
plt.plot(t, initial_solution[:, 1], 'r--', label='Predicted (No Control)')
plt.axvline(x=20, color='k', linestyle=':')
plt.xlabel('t')
plt.ylabel('감염자수 I(t)')
plt.legend()
plt.title('SIR 모델 예측')
# 두 번째 그래프 (R_t 변화 적용)
plt.subplot(1, 2, 2)
colors = ['r', 'b', 'g', 'm']
for i, (rt, sol) in enumerate(zip(Rt_values, solutions)):
plt.plot(t, sol[:, 1], colors[i], label=f'R_t={rt}')
plt.axvline(x=20, color='k', linestyle=':')
plt.xlabel('t')
plt.ylabel('감염자수 I(t)')
plt.legend()
plt.title('SIR 모델 통제')
plt.tight_layout()
plt.show()
복잡한 모형으로
앞서 설명한 것처럼 현상을 적절하게 나타내는 좋은 모형일수록, 실제 현상을 예측하고 통제하는 데 뛰어납니다. 소개한 SIR 모형은 매우 간단하면서도 감염병의 유행을 제대로 기술할 수 있다고 알려져 있습니다.
물론 더 좋은 모형을 얻으려면 SIR 모형의 가정을 변경하고, 보다 현실적인 요소를 도입하는 것이 중요하다.
예를 들어 연령에 따른 감염률이나 회북률이 다르다, 접촉하는 상대가 무작위로 가정되있는점, 백신의 효과를 적용한 모형을 이용하면, 백신이 감염병 비율 움직임에 어떠한 영향을 주는지 조사도 가능하다.
수리 모형 : 확률 모형
확률 모형
결정론이라도 요소의 수가 너무 많은 나머지 결정론 모형으로 다루기가 어려워, 확률을 이용하여 통계적으로 다루게 되었다.
무작위 행보
가장 간단한 확률 모형의 예인 무작위 행보(random walk)를 살펴봅시다.
import numpy as np
import matplotlib.pyplot as plt
# 무작위 행보 설정
np.random.seed(42) # 재현 가능성을 위해 시드 설정
n_steps = 1000 # 총 이동 횟수
n_walks = 10 # 여러 개의 무작위 행보 생성
plt.figure(figsize=(10, 5))
for i in range(n_walks):
steps = np.random.choice([-1, 1], size=n_steps) # -1 또는 +1 중 무작위 선택
position = np.cumsum(steps) # 위치 추적
plt.plot(position, label=f'Walk {i+1}')
plt.axhline(0, color='black', linestyle='--', linewidth=0.8)
plt.axvline(0, color='black', linestyle='--', linewidth=0.8)
plt.xlabel('Steps')
plt.ylabel('Position')
plt.title('Multiple 1D Random Walks')
plt.legend()
plt.show()
기대값은 0이다. 그러나 시간이 흐를수록 점점 큰 값이나 작은 값이 나타나는 일이 늘어난다. 가로 축이 충분히 있으면
분포는 평균 100, 표준편차 $ \sigma \sqrt{t} $ 인 정규분포로 근사할 수 있다.
이처럼 확률적으로 시간 변동하는 현상을 기술하는 수리모형을, 확률 과정이라 한다.
마르코프 과정
무작위 행보를 일반화한 확률 과정으로 마르코프 과정(Markov process)이 있습니다.
마르코프 과정은 과거 상태와는 상관없이, 현재 상태에 따라 결정되는 확률 과정입니다.
이 과거와 상관없이 현재 상태에 따라 미래가 정해지는 성질을 마르코프 성질이라 합니다.
무작위 행보에서 도박의 승패는 과거의 어떤 사건과도 상관없이 정해지므로(정해진다고 가정하므로),
마르코프 성질이 있다고 할 수 있습니다.
$$ Q = \begin{bmatrix}
0.5 & 0.3 & 0.2 \\
0.5 & 0.2 & 0.3 \\
0.1 & 0.5 & 0.4 \\
\end{bmatrix} $$
마르코프 과정의 예를 자주 드는 것이 날씨입니다.
날씨 상태에는 {맑음, 흐림, 비}의 3가지 이산적인 상태가 있으며 시간도 어제, 오늘, 내일과 같이 이산적적이라 하면. 그러면 오늘 날씨로부터 내일 날씨로 변하는 과정을
이를 전이행렬(transition matrix)이라 합니다.
수리 모형의 역할
수학은 인간의 일상 감각이 다다르지 못하는 곳으로 우리를 데려다주는 도구라고 할 수 있다.
물론 모형은 실제 현상의 일부만을 취해, 사람이 세운 가정을 이용하여 만든 것임을 잊어서는 안된다.
현실 세계의 현상을 어느 정도 예측할 수 있는지의 관점에서 끊임없이 모형의 좋고 나쁨을 평가하고,
그 결과를 바탕으로 모형을 개선하는 노력을 게을리 하지 않도록 합시다.
'Statistics' 카테고리의 다른 글
| [통계 101 x 데이터 분석] 통계분석과 관련된 그 밖의 방법 (0) | 2025.02.06 |
|---|---|
| [통계 101 x 데이터 분석] 베이즈 통계 (1) | 2025.02.06 |
| [통계 101 x 데이터 분석] 인과와 상관 (0) | 2025.02.06 |
| [통계 101 x 데이터 분석] 가설검정의 주의점 (0) | 2025.02.05 |
| [통계 101 x 데이터 분석] 통계 모형화 (3) | 2025.02.01 |

