| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- TiL
- 내일배움캠프
- 티스토리챌린지
- 스파르타코딩
- 스파르타
- MySQL
- wil
- 오블완
- 웹 스크랩핑
- hackerrank
- 파이썬
- SQL
- Cluster
- 파이썬 머신러닝 완벽 가이드
- 프로그래머스
- 미세먼지
- 파이썬 머신러닝 완벽가이드
- 파이썬 완벽 가이드
- harkerrank
- 프로젝트
- 파이썬 철저 입문
- 텍스트 분석
- 회귀분석
- 파이썬 철저입문
- 스파르타 코딩
- 내일배움
- 중회귀모형
- 내일배움카드
- R
- 실전 데이터 분석 프로젝트
- Today
- Total
OkBublewrap
[통계 101 x 데이터 분석] 베이즈 통계 본문
통계학의 2가지 흐름
1. 빈도주의 통계
2. 베이즈 통계
불확실성 다루기
통계학은 불확실성을 다루고자 확률을 이용합니다. 지금까지 등장한 빈도주의 흐름에서의 불확실성은, 모집단엣 표본을 추출할 때의 불확실성입니다.
빈도주의
무한히 반복 실행한 결과로써의 객관적인 빈도를 나타냅니다.
베이즈 통계
확률을 얼마나 확신하는지로 해석하는 원리
통계 모형
통계 모형의 목적과 방침은 지금까지 소개한 방법들과 똑같이, 데이터의 발생원인 모집단의 실제 분포 q(x)를 아는 것입니다.
그런데 q(x)를 직접 알기는 불가능하므로, 얻은 데이터 x1, x2, ..., xn으로부터 분포 q(x)을 추론해 가는 방법을 이용한다.
이처럼 데이터로 모집단의 실제 분포 q(x)를 추론하는 것을 통계적 추론이라고 합니다.
데이터를 이용하여 추정한 통계 모형 p(x)가 모집단의 실제 분포 q(x)와 어느 정도 들어맞는지 정량화함으로써, 통계 모형 적합도를 평가할 수 있다.
베이즈 통계의 사고방식
베이즈 통계에서는 통계 모형의 파라미터를 확률변수로 취급하여, 그 확률분포를 생각합니다.
1. 분석자가 데이터를 알기 전 단계의 확률분포. 사전분포 준비
2. 사후분포 구하기
$$ P(A \mid B) = \frac{P(B \mid A) P(A)}{P(B)} $$
베이즈 통계는 사전분포와 가능도에서 사후분포를 구하는 것이 목적입니다.
분모를 직접 구하기는 어려운 경우가 많다. 이떄는 나중에 설명할 MCMC방법이란 난수 발생 알고리즘을 대신 이용하여, 근사적으로 사후분포를 구한다.
사전분포
사전분포는 데이터를 얻기 전에 파라미터가 어떤 분포인가를 미리 실험자나 해석자가 설정해야 하는 분포입니다.
베이즈 추정에서 균등분포를 무정보 사전분포로 이용하곤한다.
베이즈 추정의 예측 분포
베이즈 추정으로 얻은 파라미터의 사후분포로 예측분포를 만들 수 있다.
$$ p(x^* \mid D) = \int p(x^* \mid \theta) p(\theta \mid D) d\theta $$
정보량 기준
실제 모집단 분포 q(x)와 예측분포 p(x)가 어느 정도 일치하는가를 평가할 때는 2개의 확률밀도함수 f(x)와 g(x)를 비교하는 쿨백-라이블러 발산을 이용합니다.
$$ D(f \parallel g) = \int f(x) \log \frac{f(x)}{g(x)} dx $$
이 식의 결과는 f(x)와 g(x)가 가까울수록 작은 값이 됩니다. 항상 0보다 크거나 같으며, 임의의 x에 대해 f(x)=g(x)일 때, D(f||g)=0인 성질을 가집니다.
가능도 추정에서 $ D(q(x) || p^{*}(x)) $를 작게 하는 것은
AIC를 작게 만드는 것과 같다.
AIC와 같은 모형의 좋고 나쁨을 평가하는 지표를 정보량 기준이라 한다.
베이즈 추정의 경우 WAIC(Widely Applicable Information Criteria)를 작게 하는 것과 같습니다.
베이즈 통계의 이점
1. 추정 결과, 통계 모형의 파라미터를 분포로 얻을 수 있다는 점입니다.
2. MCMC 방법이 난수를 발생시켜 시뮬레이션으로서 사후분포를 따르는 파라미터를 얻기 때문에 복잡한 모형화가 가능하다는 점이 있습니다.
단, MCMC 방법은 난수를 이용한 시뮬레이션의 일종이므로, 완전히 동일한 데이터라도 해석 결과가 조금씩 달라진다.
추정이 잘되었을 때는 거의 무시할 정도로 결과 차이가 작다
베이즈 통계 알고리즘
MCMC 방법
특정 확률분포를 따르는 난수 발생 알고리즘입니다.
베이즈 통계에서는 이것을 이용하여 사후분포를 따르는 난수를 발생시키고, 그 난수의 집합을 관찰함으로써
사후 분포의 성질을 분석합니다.
몬테카를로 방법
난수를 여러 개 발생시켜 시뮬레이션해 근사해를 얻는 방법.
import numpy as np
import matplotlib.pyplot as plt
# 시뮬레이션할 점 개수
N = 10000
# x, y 좌표를 [-1, 1] 범위에서 무작위 생성
x = np.random.uniform(-1, 1, N)
y = np.random.uniform(-1, 1, N)
# 원 안에 포함된 점 판별 (x^2 + y^2 ≤ 1)
inside = x**2 + y**2 <= 1
# 원 안과 밖의 점을 분리
x_inside, y_inside = x[inside], y[inside]
x_outside, y_outside = x[~inside], y[~inside]
# π 값 근사
pi_estimate = 4 * np.sum(inside) / N
print(f"근사한 원주율 값: {pi_estimate:.5f}")
# 그래프 그리기
fig, ax = plt.subplots(figsize=(6, 6))
ax.scatter(x_inside, y_inside, color='blue', s=1, label="inner")
ax.scatter(x_outside, y_outside, color='red', s=1, label="outer")
# 원과 정사각형의 경계를 그림
circle = plt.Circle((0, 0), 1, color='black', fill=False)
ax.add_patch(circle)
ax.set_xlim(-1, 1)
ax.set_ylim(-1, 1)
ax.set_aspect('equal')
ax.set_title(f"{pi_estimate:.5f}")
ax.legend()
plt.show()
-1 ~ 1 사이의 균등분포에서 (x, y)의 난수를 발생시켜, 원안에 있는 난수의 개수를 세면 원주율은 근사적으로 구할 수 있다.
마르코프 연쇄
어떤 상태에서 다른 상태로 변화하는 현상을 확률로 표현한 모형의 일종
MCMC 방법의 예
마르코프 연쇄와 몬테카를로 방법 두 가지를 조합하여, 사후분포를 따르는 값을 표집
구체적인 계산은 한쪽 변수를 고정한 뒤, 고정하지 않은 변수를 확률적으로 움직이는 작업을 번갈아 반복하는
순서로 이루어집니다.
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
# 2차원 정규분포의 평균과 공분산 행렬 설정
mu_x, mu_y = 0, 0 # 평균
sigma_x, sigma_y = 1, 1 # 표준편차
rho = 0.8 # x와 y 사이의 상관 계수
# 공분산 행렬
cov_matrix = [[sigma_x**2, rho * sigma_x * sigma_y],
[rho * sigma_x * sigma_y, sigma_y**2]]
# 2차원 정규분포에서 직접 샘플링 (비교용)
true_samples = np.random.multivariate_normal([mu_x, mu_y], cov_matrix, 10000)
# 깁스 샘플링을 이용한 난수 생성
def gibbs_sampling(N, burn_in=1000):
samples = np.zeros((N + burn_in, 2))
x, y = 0, 0 # 초기값 설정
for i in range(N + burn_in):
# x를 y에 대한 조건부 분포에서 샘플링
mu_x_given_y = mu_x + rho * (sigma_x / sigma_y) * (y - mu_y)
sigma_x_given_y = np.sqrt((1 - rho**2) * sigma_x**2)
x = np.random.normal(mu_x_given_y, sigma_x_given_y)
# y를 x에 대한 조건부 분포에서 샘플링
mu_y_given_x = mu_y + rho * (sigma_y / sigma_x) * (x - mu_x)
sigma_y_given_x = np.sqrt((1 - rho**2) * sigma_y**2)
y = np.random.normal(mu_y_given_x, sigma_y_given_x)
samples[i] = [x, y]
return samples[burn_in:] # 초기 burn-in 기간 제외
# 깁스 샘플링 수행
N_samples = 10000
gibbs_samples = gibbs_sampling(N_samples)
# 그래프 출력
fig, ax = plt.subplots(1, 2, figsize=(12, 5))
# 직접 샘플링한 2차원 정규분포
ax[0].scatter(true_samples[:, 0], true_samples[:, 1], alpha=0.3, s=2, color='blue')
ax[0].set_title("2D Normal Distribution")
ax[0].set_xlabel("X")
ax[0].set_ylabel("Y")
# 깁스 샘플링한 결과
ax[1].scatter(gibbs_samples[:, 0], gibbs_samples[:, 1], alpha=0.3, s=2, color='red')
ax[1].set_title("Gibbs Sampling")
ax[1].set_xlabel("X")
ax[1].set_ylabel("Y")
plt.tight_layout()
plt.show()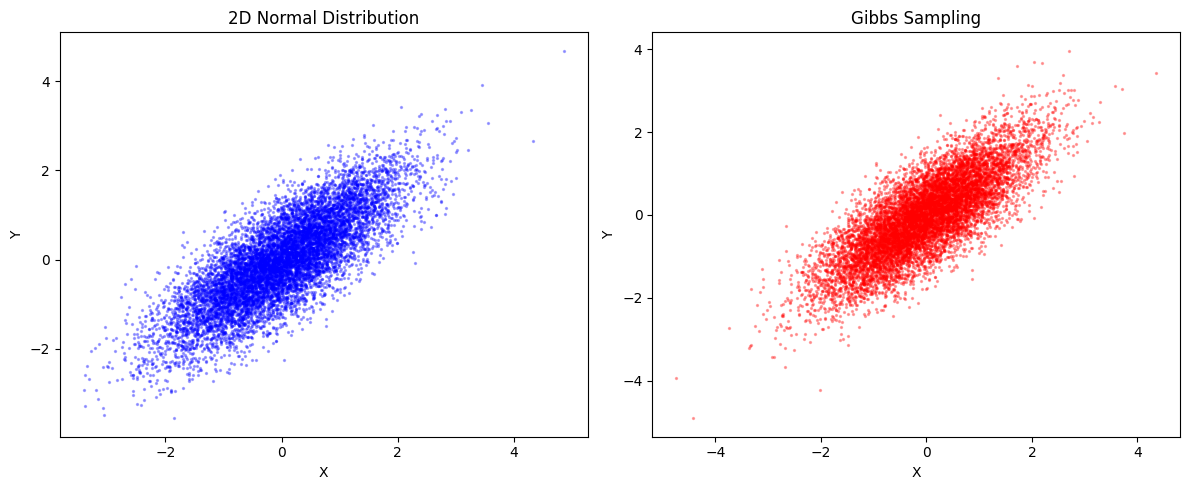
그 외에도 메트로폴리스-헤이스팅스 알고리즘, 해미토니안 몬테카를로 방법이 있다.
베이즈 통계 사례
이평균 t-test 예제
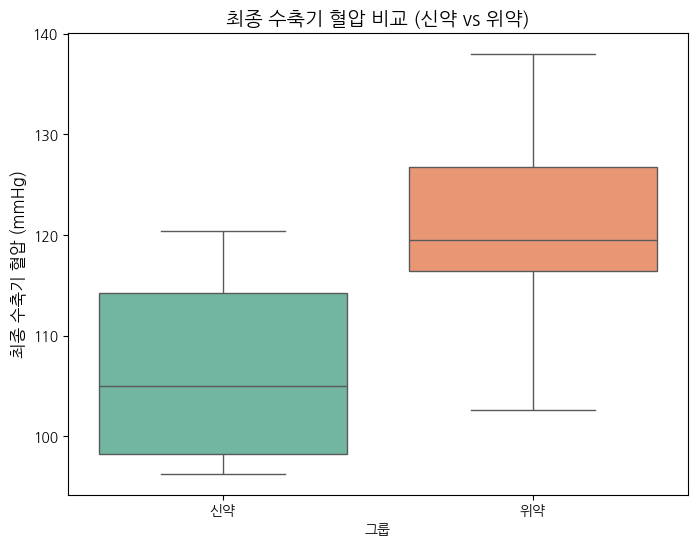
T 통계량 -3. 15, p값 : 0.0055
MCMC
import numpy as np
import matplotlib.pyplot as plt
plt.rcParmas['axes.unicode_minus'] = False
# 예시 데이터 생성 (이전에 만든 데이터 사용)
np.random.seed(42)
systolic_treatment = np.array([116.9, 120.5, 127.5, 135.4, 118.6, 118.6, 138.0, 129.6, 118.0, 120.4,
115.7, 106.3, 124.7, 102.6, 96.3, 115.9, 103.7, 124.4, 111.0, 96.5])
systolic_placebo = np.array([120.5, 127.5, 135.4, 118.6, 118.6, 138.0, 129.6, 118.0, 120.4, 115.7,
106.3, 124.7, 102.6, 96.3, 115.9, 103.7, 124.4, 111.0, 96.5])
# MCMC 샘플링 설정
n_samples = 10000
mu_diff_samples = []
# 초기 값 설정
mu_treatment_current = np.mean(systolic_treatment)
mu_placebo_current = np.mean(systolic_placebo)
# MCMC 샘플링 루프 (Metropolis-Hastings 알고리즘)
for _ in range(n_samples):
# 제안 분포에서 새 샘플을 제시
mu_treatment_proposed = np.random.normal(mu_treatment_current, 1)
mu_placebo_proposed = np.random.normal(mu_placebo_current, 1)
# 제시된 값에서 우도 계산
log_likelihood_current = -0.5 * np.sum((systolic_treatment - mu_treatment_current)**2) - 0.5 * np.sum((systolic_placebo - mu_placebo_current)**2)
log_likelihood_proposed = -0.5 * np.sum((systolic_treatment - mu_treatment_proposed)**2) - 0.5 * np.sum((systolic_placebo - mu_placebo_proposed)**2)
# Metropolis-Hastings 수락 기준
acceptance_ratio = np.exp(log_likelihood_proposed - log_likelihood_current)
if np.random.rand() < acceptance_ratio:
mu_treatment_current = mu_treatment_proposed
mu_placebo_current = mu_placebo_proposed
# 평균 차이 저장
mu_diff_samples.append(mu_treatment_current - mu_placebo_current)
# 결과 시각화
mu_diff_samples = np.array(mu_diff_samples)
plt.figure(figsize=(8, 6))
plt.hist(mu_diff_samples, bins=50, density=True, color='skyblue', edgecolor='black')
plt.title('Bayesian Estimation of Mean Difference (Treatment - Placebo)', fontsize=14)
plt.xlabel('Mean Difference (Treatment - Placebo)', fontsize=12)
plt.ylabel('Density', fontsize=12)
plt.show()
# 95% 신뢰 구간 계산
lower_bound = np.percentile(mu_diff_samples, 2.5)
upper_bound = np.percentile(mu_diff_samples, 97.5)
print(f"95% 신뢰 구간: ({lower_bound:.2f}, {upper_bound:.2f})")
예시 데이터로 만든 위약, 신약은 95% 신뢰구간이 (-0.63, 0.67)으로 차이가 0을 포함하고 있으므로, 신약과 위약 간에 효과 차이가 없다고 결론을 낼 수 있다.
'Statistics' 카테고리의 다른 글
| [통계 101 x 데이터 분석] 모형 (0) | 2025.02.07 |
|---|---|
| [통계 101 x 데이터 분석] 통계분석과 관련된 그 밖의 방법 (0) | 2025.02.06 |
| [통계 101 x 데이터 분석] 인과와 상관 (0) | 2025.02.06 |
| [통계 101 x 데이터 분석] 가설검정의 주의점 (0) | 2025.02.05 |
| [통계 101 x 데이터 분석] 통계 모형화 (3) | 2025.02.01 |

