| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- Cluster
- 프로그래머스
- 스파르타 코딩
- 내일배움캠프
- hackerrank
- 미세먼지
- 파이썬 머신러닝 완벽가이드
- R
- 파이썬 완벽 가이드
- 티스토리챌린지
- 중회귀모형
- 내일배움카드
- TiL
- 파이썬
- 웹 스크랩핑
- 파이썬 철저 입문
- 프로젝트
- 오블완
- 내일배움
- 회귀분석
- 실전 데이터 분석 프로젝트
- wil
- SQL
- 스파르타코딩
- 파이썬 머신러닝 완벽 가이드
- 텍스트 분석
- 파이썬 철저입문
- MySQL
- 스파르타
- harkerrank
- Today
- Total
OkBublewrap
[통계 101 x 데이터 분석] 상관과 회귀 본문
양적 변수 사이 관계를 밝히다
2개의 양적 변수로 이루어진 데이터
양적 변수 사이의 관계를 분석하는 또 다른 방법인 상관과 회귀를 설명
산점도

상관
산점도를 이용하면 두 양적 변수의 관계를 시각화하면 어떤 관계가 있는지 대략적으로 파악할 수 있습니다.
위 그림을 보면 수학점수가 오르면 과학점수도 높은 경향이 있다는 것을 확인할 수 있습니다.

그림으로 살펴본 2개 변수 사이의 관계성을 상관이라 합니다
이는 2개의 확률변수 또는 데이터 사이의 관계성을 의미합니다.
⚠️ 상관이 있다고 해서 원인과 결과를 뜻하는 인과관계가 있는지까지는 알 수 없다.
회귀
$ y=f(x) $ 함수를 통해 변수 사이의 관계를 공식화 하는 것을 가르킵니다.
여기서 x를 설명변수, 독립변수, y를 반응변수 또는 종속변수라고 한다.

상관관계
피어슨 상관계수
위 그림으로 관계성이 어느정도로 강한지를 수치로 나타낼 수 있다면, 대상을 이해하는 데 도움이 됩니다. 위 그림의 예시로 과학 점수를 올리기 위해서는 기초적인 수학 능력으르 기르는 것이 중요하다라는 하나의 가능성을 떠올릴 수 있습니다.
이는 가능성인 것을 명심해야 합니다.
$$ r = \frac{\sum{(x_i - \bar{x})(y_i - \bar{y})}}{\sqrt{\sum{(x_i - \bar{x})^2} \cdot \sum{(y_i - \bar{y})^2}}} $$

피어슨 상관계수 부호가 양일 때는 x가 커질수록 y도 함께 커지고, x가 작아질수록 y가 작아지는 관계성을 양의 상관관계라고 합니다. 반대로 부호가 음일 때 음의 상관관계라고 합니다.
$ 0.7 < \left | r\right | \leq 1 $ : 강한 상관
$ 0.4 < \left | r\right | \leq 0.7 $ : 중간 정도 상관
$ 0.2 < \left | r\right | \leq 0.4 $ : 약한 상관
$ 0.0 < \left | r\right | \leq 0.2 $ : 거의 상관없음
상관관계는 r은 선형관계를 나타난다.
비선형관계는 피어슨 상관관계로 적절하게 정량화할 수 없다.
또한 직선의 기울기 크기와는 관계가 없다(선형 관계성의 강도만 정량화)
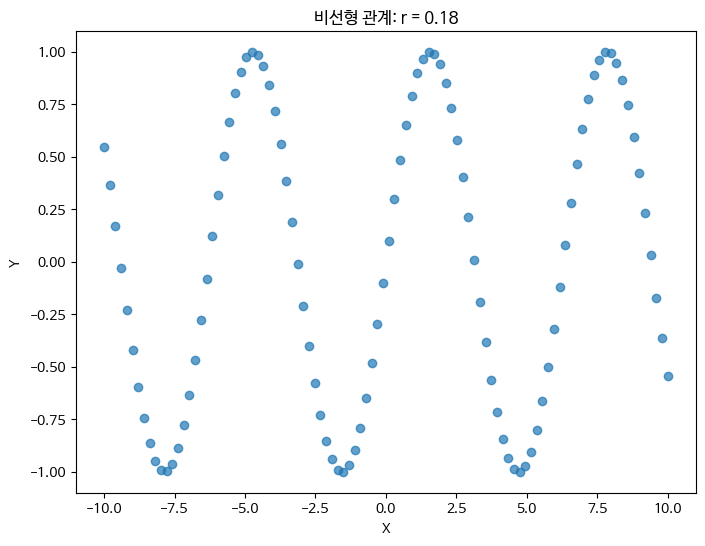
상관계수가 같은 다양한 데이터
같은 r값을 가지고 있더라도, 비선형을 포함해 다양한 패턴이 있을 수 있다.
데이터 셋
Data from: Matejka, J., & Fitzmaurice, G. (2017, May). Same stats, different graphs: generating datasets with varied appearance
Data from: Matejka, J., & Fitzmaurice, G. (2017, May). Same stats, different graphs: generating datasets with varied appearance and identical statistics through simulated annealing. In Proceedi...
gist.github.com

⚠️ 데이터로 상관계수를 계산하기만 하고서, 데이터가 전형적인 우상향 산점도가 되리라 짐작하는 것은 위험하다
정규성 검사
피어슨 상관계수 r은 평균이나 분산에 기반한 모수적인 방법이므로, x의 분포, y의 분포가 모두 정규분포라고 가정
따라서 데이터가 좌우로 찌그러지거나, 쌍봉형이거나, 데이터에 이상값이 있을 때 적절하지 않다.

⚠️ 실전에서는 상관계수를 계산하기 전에 x축 데이터와 y축 데이터 각각에 대해 정규성을 샤피로-윌크 검정 등으로 확인한 다음, 한쪽에 조금이라도 정규성이 없다면 다음에 소개하는 비모수 상관계수를 이용하는 것이 좋습니다
비모수 상관계수
x축, y축 중 적어도 하나 이상에 정규성이 없을 때는, 비모수 상관계수인 스피어만 순위상관계수 사용이 권장된다.
이상치가 상관계수에 영향을 끼치는 그림에서 스피어만 순위상관계수를 사용하게 되면, 이상치 없을 때(왼쪽)은 -0.11, 이상치 있을 때(오른쪽) -0.08로 결과에 거의 영향을 주지 않는 사실!
켄달 순위상관계수 : 스피어만 순위상관계수와 사용 대상은 거의 비슷하나, 표본크기가 매우 작을 때 켄달 순위상관계수쪽이 나중에 설명할 유의성검정의 관점에서 더 좋다고 한다.
상관관계 사용시 주의할 점
상관관계를 계산할 때 2개 변수가 처음부터 종속 관계일 때는 주의가 필요하다.


X, Y 관계가 무상관일 경우에도 X와 변환된 새로운 변수 Y/X는 음의 상관관계를 가진다.
상관계수와 가설
표본으로 계산한 상관계수 r의 배경으로는 상관계수 r를 갖는 2개 확률변수로 이루어진 모집단분포를 생각할 수 있다.

상관계수가 0으로 무상관이라 해도, 표본을 추출해 상관계수 r을 계산하면 정확히 0이 되지 않고 0을 중심으로 퍼진 분포로 나타난다.

가령 표본의 상관계수로 r=0.5을 얻었다 하더라도, 모집단의 상관계수에서도 0.5 정도의 상관계수가 나타나는 것이라면, 귀무가설은 기각할 수 없습니다. 가설검정을 시행한 결과 p<0.05임을 알고 나서야 비로소 양의 상관이 있다고 주장 가능합니다.
표본크기와 가설검정
표본크기 n이 무척 클 때는 가설 검정의 결과 해석에 주의해야 합니다. 가설 검정에서는 표본크기 n이 클수록 모집단이 귀무가설에서 아주 조금만 어긋나더라도 p값이 작아져 통계적으로 유의미하다고 판단됩니다.
⚠️ r과 p 양쪽 모두를 보고 해석하는 것이 중요
p<0.05라고 해서 곧바로 상관이 있다고 판단하는 것이 아니라, r값 자체에 눈을 돌려 그 크기를 해석할 필요가 있다.
비선형상관
X가 Y에 관해,
또는 Y가 X에 관해 어느 정도의 정보를 포함하는지의 관점에서 관계성 강도를 정량화하는 것.
예를 들어 피어슨 상관계수가 1일 때 X를 알면 Y의 값도 완전하게 알 수 있다는 점,
X에는 Y에 관한 정보가 있다고 할 수 있습니다.
선형회귀
회귀란 설명변수 x와 반응변수 y사이에 $ y = f(x) $라는 함수를 적용시키는 것을 일컫습니다.
회귀식형태를 결정하는 파라미터 a, b를 회귀계수라 합니다.
특정 평가기준에 따라 회귀의 좋음을 평가하고,
이 회귀 계수의 값을 구체적으로 구하는 것이 회귀분석의 큰 흐름이다.
$$ y = a + bx + \varepsilon $$
여기서 a나 b는 모집단의 성질을 나타내는 파라미터로, 아직 미지수이다.
그렇기 때문에 표본에서 이들 파라미터를 추정하는 것이 목표이다.
- 어떤 회귀식을 적용할 것인가?
- 어떻게 회귀식을 데이터에 적용할 것인가?
- 얻은 회귀모형을 어떻게 평가할 것인가?
데이터에 가능한 한 들어맞는 회귀모형이 좋은 모형이라고 생각합시다.
가능한 한 들어맞는을 다른 말로 하면, 데이터와 회귀식의 차이가 가능한 한 작은이 됩니다.
데이터와 모형 차이가의 제곱을 모두 더한 값 E를 최소화하는 방법을 최소제곱법이라 한다.
어떻게 하더라도 회귀직선이 모든 데이터 점을 통과할 수는 없습니다.
이를 확률오차 $ \varepsilon $ 으로 표현합니다.
회귀계수
최소제곱법으로 얻은 회귀계수을 이용하여 회귀 계수 $ \widehat{a} $ 와 $ \widehat{b} $은 모집단 파라미터 a와 b의 비편향추정량이 됩니다.
$ E(\widehat{a}) = a $
$ E(\widehat{b}) = b $
각각의 값은 a나 b에서 벗어날 수 있으나 평균적으로 과대평가하거나 과소평가하지 않는 추정량입니다.
최소제곱법으로 얻은 추정량은 비편향추정량 중에서도 가장 정밀도가 높은(분산이 작은) 비편향추정량이 됩니다.
이를 최량선형비편향추정량이라하며,
가우스-마르코프 정리가 이를 증명합니다.
최소제곱법
단순선형회귀모형(simple linear regression model) 이렇게 회귀모형을 설정하고 분석하는 것을 회귀분석이라 한다.회귀분석은 변수들로 예측될 수 있도록 이용하는 통계적방법이다. 모수로 추
okbublewrap.tistory.com
최량선형불편추정량
최량선형불편추정량 Best Linea Unbiased Estimator : BLUE : 모든 추정량 중에서 관측치들의 선형 결합으로 이루어진 추정량이어야 하고 불편성을 만족하며 최소 분산을 갖는 추정량 모회귀계수 베타0와
okbublewrap.tistory.com
회귀계수의 가설검정
회귀계수를 대상으로 가설검정을 시행할 수 있습니다.
이 경우 앞서 설명한 오차의 가정에 더해, 오차의 분포가 정규분포라고 추가로 가정해야 합니다.
단, 표본크기이 충분히 클 때는 오차항이 정규분포를 따르지 않아도 가설검정을 시행할 수 있습니다.
95% 신뢰구간, 95% 예측구간

- Regression Line : 회귀선, 데이터를 기반으로 추정한 선형회귀선
- 95% Confidence Interval : 신뢰구간, X값에서 평균 Y값의 신뢰도(95%)
- 95% Prediction Interval :
예측구간, 새로운 데이터가 들어올 때 그 범위를 예상하고자 할 때 사용. 분산이크면 범위가 더 넓어짐
결정계수
최소제곱법으로 데이터에 아무리 잘 들어맞는 회귀식을 구하더라도 데이터와 회귀식이 꼭 들어맞지는 않습니다.
이는 확률적인 변동을 포함한 다른 요인이 있기 때문이며, 회귀식만으로 반응변수 전부를 설명할 수 없다는 데서 기인합니다.
회귀식이 잘 들어맞는지 평가하는 지표로, 결정계수 $ R^2 $을 자주 사용합니다.
- 결정계수가 1에 가까울수록 회귀모형이 데이터에 잘 들어맞음
- 0에 가까울수록 잘 들어맞지 않음을 의미

⚠️ 그러나 결정계수는 설명변수의 개수가 늘어날수록 커지는 성질이 있는 까닭에, 의미없는 설명변수를 도입하면 실제론 그렇지 않은데도 일견 회귀모형의 설명력이 향상된 것처럼 보일 수 있습니다. 따라서 설명변수 개수 k에 따라 조정한 수정된 결정계수를 사용하는 것이 일반적입니다.
오차의 등분산성과 정규성

현재 그래픠의 잔차의 정규성과 등분산성을 만족하는 그래프이다.
- 오차항이 정규분포를 따르고 있는지 여부느, 데이터와 모형의 차이인 잔차의 정규성을 샤피로-윌크 검정을 통해 확인하면 알 수 있습니다.
- 등분산성을 확인하려면 설명변수 x가 변할 때 잔차의 분산이 달라지는지를 조사하는 브루쉬-페이건 검정을 이용합니다.
설명변수와 반응변수
상관과 달리 회귀에는 설명변수 x와 반응변수 y라는 비대칭성이 있다.
그러므로 분석을 하기 전에 무엇을 설명변수로 하고 무엇을 반응변수로 할 것인가를 목적에 맞게 생각해야 한다.
- 한쪽 변수로 다른 한쪽 변수를 설명하고자 할때
설명하는 쪽을 설명변수, 설명할 대상을 반응변수로 설정 - 인과효과를 알고 싶을 때
원인을 설명변수로, 결과를 반응변수로 설정합니다. 단, 충분히 유의해야 할점이 있습니다.
인과효과를 올바르게 추정하기 위해서는, 서로 다른 x에 대해 그 밖의 요인이 같아야만 합니다. 따라서 설명변수를 무작위로 할당한 개입 실험에서 얻은 데이터나, 상정할 수 있는 다른 요인도 포함한 다중회귀모형 등을 이용하는 것이 필요합니다. - 데이터를 예측하고 싶을 때
예측의 근거가 될 변수를 설명변수, 예측하고자 하는 변수를 반응변수로 설정합니다. 그럼 회귀분석의 결과로 얻은 회귀모형에 새롭게 얻은 설명변수 값을 대입하여 반응변수 값을 예측할 수 있습니다.
'Statistics' 카테고리의 다른 글
| [통계 101 x 데이터 분석] 가설검정의 주의점 (0) | 2025.02.05 |
|---|---|
| [통계 101 x 데이터 분석] 통계 모형화 (3) | 2025.02.01 |
| [통계 101 x 데이터 분석] 다양한 가설 검정 (0) | 2025.01.23 |
| [통계 101 x 데이터 분석] 가설검증 (1) | 2025.01.22 |
| [통계 101 x 데이터 분석] 추론통계 ~ 신뢰구간 (0) | 2025.01.21 |
