| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 스파르타코딩
- 오블완
- SQL
- harkerrank
- 파이썬 철저입문
- wil
- R
- 파이썬 머신러닝 완벽 가이드
- Cluster
- 내일배움카드
- 회귀분석
- 파이썬
- 실전 데이터 분석 프로젝트
- 스파르타
- TiL
- 내일배움
- MySQL
- 웹 스크랩핑
- hackerrank
- 프로젝트
- 파이썬 완벽 가이드
- 중회귀모형
- 내일배움캠프
- 프로그래머스
- 파이썬 철저 입문
- 파이썬 머신러닝 완벽가이드
- 티스토리챌린지
- 스파르타 코딩
- 텍스트 분석
- 미세먼지
- Today
- Total
OkBublewrap
[통계 101 x 데이터 분석] 다양한 가설 검정 본문
가설검정 방법 구분해 사용하기
가설검정 해석 흐름
어느 가설검정 방법이든 간에 해석의 기본 흐름은 공통
- 귀무가설 설정 : 확인하고 싶은 대상에 따라 귀무가설과 대립가설을 설정
- 데이터로 검정통계량 계산 : 데이터로 가설검정에 필요한 검정통계량을 계산
- 귀무가설이 옳다는 가정하에 통계량의 분포를 생각하고, 데이터로 계산한 통계량이 분포의 어느 위치에 있는지 구하여 P값을 계산한다.
✅ 가설 검정 방법을 선택할 때는 다음에 설명하는 데이터 유형, 표본의 수, 양적 변수 분포의 성질을 먼저 확인
데이터 유형에 따라 달라지는 해석 방법
import seaborn as sns
import matplotlib.pyplot as plt
import pandas as pd
# 데이터 로드
df = sns.load_dataset('tips')
# 서브플롯 생성 (1행 3열)
fig, axes = plt.subplots(1, 3, figsize=(18, 6), sharey=False)
# 첫 번째 서브플롯: Barplot
sns.barplot(data=df, x='sex', y='total_bill', ax=axes[0])
axes[0].set_title('Barplot of Total Bill by Sex')
# 두 번째 서브플롯: Crosstab을 Heatmap으로 시각화
crosstab = pd.crosstab(df['sex'], df['smoker'])
sns.heatmap(crosstab, annot=True, fmt='d', cmap='coolwarm', ax=axes[1])
axes[1].set_title('Crosstab of Sex and Smoker')
# 세 번째 서브플롯: Scatterplot
sns.scatterplot(data=df, x='total_bill', y='tip', ax=axes[2])
axes[2].set_title('Scatterplot of Tip vs Total Bill')
# 레이아웃 조정
plt.tight_layout()
plt.show()
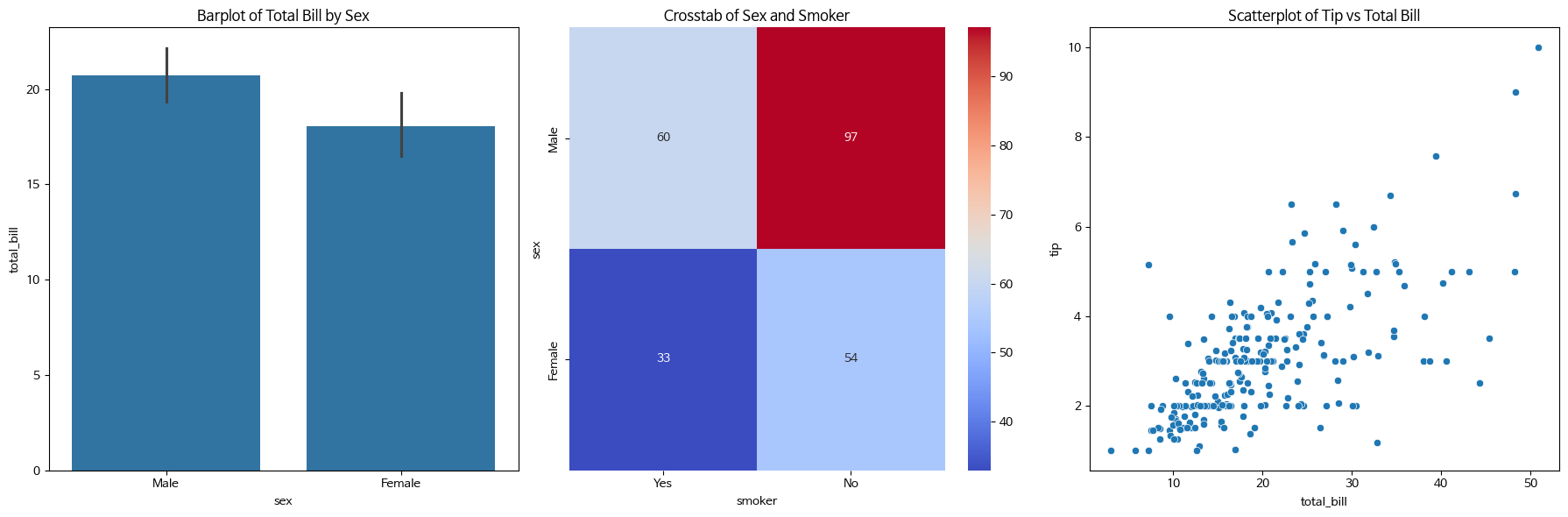
- 범주형(성별) - 양적(총 지불금액)
- 범주형(성별) - 범주형(흡연 유무) : 분할표
- 양적(총 지불 금액) - 양적(서비스 지불 금액) : 산점도
어느 쪽이든 데이터 유형이 양적변수인지 질적 변수인지에 따라 해석 방법이 달라지니, 먼저 데이터 유형부터 확인
표본의 수
표본의 수(집단의 수)도 분석 방법 선택에서 중요한 요소 입니다.
import seaborn as sns
import matplotlib.pyplot as plt
# 데이터 로드
df = sns.load_dataset('tips')
# 서브플롯 생성 (1행 3열)
fig, axes = plt.subplots(1, 3, figsize=(18, 6), gridspec_kw={'width_ratios': [1, 2, 2]}, sharey=True)
# 첫 번째 서브플롯: 전체 Total Bill의 Barplot (축소)
sns.barplot(data=df, y='total_bill', ax=axes[0], color='pink')
axes[0].set_title('Barplot of Total Bill')
axes[0].set_xlabel('')
axes[0].set_ylabel('Total Bill')
# 두 번째 서브플롯: 성별에 따른 Total Bill의 Barplot
sns.barplot(data=df, x='sex', y='total_bill', ax=axes[1], color='g')
axes[1].set_title('Barplot by Sex')
# 세 번째 서브플롯: 요일별 Total Bill의 Barplot
sns.barplot(data=df, x='day', y='total_bill', ax=axes[2], color='y')
axes[2].set_title('Barplot by Day')
# 레이아웃 조정
plt.tight_layout()
plt.show()
왼쪽 부터 1 표본, 2표본, 4표본
2표본 이상일 때는 표본끼리 비교할 수 있으므로, 집단 간의 차이를 조사할 수 있음
3개 이상은 다중 비교라 불리는 검정이 필요
양적 변수의 성질
✅ 데이터에 양적 변수가 있는 경우, 이것이 어떤 분포를 취하는지가 검정 방법을 선택할 때 중요합니다.
t 검정은 데이터가 발생한 모집단이 정규분포라고 가정한 방법
이처럼 모집단이 수학적으로 다룰 수 있는 특정 분포를 따른다는 가정을 둔 가설검정을 모수검정이라 한다.
모수검정의 대부분은 모집단 분포가 정규분포인 경우
데이터가 정규분포로부터 얻어졌다고 간주할 수 있는 성질을 정규성이라 한다.
반대로 모집단 분포가 특정 분포라고 가정할 수 없는 경우 비모수검정으로 분류하는 방법을 이용
또한, 집단 간 평균값을 비교하는 경우에는 집단끼리 분산이 동일하다고 가정하는 방법이 많다.
분산이 같은 성질을 등분산성이라 한다.
데이터 정규성
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# 데이터 생성
np.random.seed(42)
# 1. 정규분포 (Normal Distribution)
normal_data = np.random.normal(loc=10, scale=2, size=1000)
# 2. 양봉형 분포 (Bi-modal Distribution)
data_bimodal = np.concatenate([np.random.normal(loc=5, scale=1, size=500),
np.random.normal(loc=15, scale=1.5, size=500)])
# 3. 좌측에 치우친 분포 (Left-skewed)
left_skewed_data = np.random.beta(a=2, b=5, size=1000) * 20
# 4. 이상치 포함 분포 (With Outliers)
data_with_outliers = np.random.normal(loc=10, scale=2, size=995)
data_with_outliers = np.append(data_with_outliers, [30, 35, 40, 50, 55]) # 이상치 추가
# 서브플롯 생성
fig, axes = plt.subplots(2, 2, figsize=(16, 12))
# 1. 정규분포 시각화
sns.histplot(normal_data, kde=True, bins=30, ax=axes[0, 0], color='blue')
axes[0, 0].set_title("Normal Distribution")
# 2. 양봉형 분포 시각화
sns.histplot(data_bimodal, kde=True, bins=30, ax=axes[0, 1], color='green')
axes[0, 1].set_title("Bi-modal Distribution")
# 3. 좌측에 치우친 분포 시각화
sns.histplot(left_skewed_data, kde=True, bins=30, ax=axes[1, 0], color='orange')
axes[1, 0].set_title("Left-skewed Distribution")
# 4. 이상치 포함 분포 시각화
sns.histplot(data_with_outliers, kde=True, bins=30, ax=axes[1, 1], color='red')
axes[1, 1].set_title("Data with Outliers")
# 레이아웃 조정 및 출력
plt.tight_layout()
plt.show()
정규성 있음 → 모수검정
정규성 없음(좌우 비대칭, 양봉형, 이상값 있음) → 비모수검정
등분산성
import numpy as np
import matplotlib.pyplot as plt
# 데이터 생성
np.random.seed(42)
# 분산이 같은 경우
group1_same_var = np.random.normal(loc=10, scale=2, size=1000) # 평균 10, 표준편차 2
group2_same_var = np.random.normal(loc=12, scale=2, size=1000) # 평균 12, 표준편차 2
# 분산이 다른 경우
group1_diff_var = np.random.normal(loc=10, scale=2, size=1000) # 평균 10, 표준편차 2
group2_diff_var = np.random.normal(loc=12, scale=5, size=1000) # 평균 12, 표준편차 5
# 서브플롯 생성
fig, axes = plt.subplots(1, 2, figsize=(18, 6), sharey=True)
# 첫 번째 서브플롯: 분산이 같은 경우
axes[0].hist(group1_same_var, bins=30, alpha=0.7, label='Group 1', color='blue')
axes[0].hist(group2_same_var, bins=30, alpha=0.7, label='Group 2', color='orange')
axes[0].set_title('Same Variance')
axes[0].set_xlabel('Value')
axes[0].set_ylabel('Frequency')
axes[0].legend()
# 두 번째 서브플롯: 분산이 다른 경우
axes[1].hist(group1_diff_var, bins=30, alpha=0.7, label='Group 1', color='blue')
axes[1].hist(group2_diff_var, bins=30, alpha=0.7, label='Group 2', color='orange')
axes[1].set_title('Different Variance')
axes[1].set_xlabel('Value')
axes[1].legend()
# 그래프 출력
plt.tight_layout()
plt.show()
1. 분산이 같음
2. 분산이 다름
대푯값 비교
모수검정의 평균값 비교
일표본 t검정
귀무가설 : 모집단의 평균 $ \mu = 0 $ 이다
대립가설 : 모집단의 평균 $ \mu = 0 $ 이 아니다
이표본 t검정
귀무가설 : 2개 집단의 평균값은 같다(평균값의 차이 = 0)
대립가설 : 2개 집단의 평균값은 다르다(평균값의 차이 ≠ 0)
t검정은 모수검정으로 분류되는 검정방법이기 때문에 데이터에 정규성이 있어야 합니다.
일반적인 t검정에서는 등분산성을 가정합니다.
분산이 일치하지 않는 경우에는 웰치의 t검정을 이용합니다. (단 정규성은 있어야 합니다.)
대응 관계가 없는 검정과 대응 관계가 있는 검정
귀무가설 : 사건 전후 차이가 없다 (D = 0)
대립가설 : 사건 전후 차이가 있다 (D ≠ 0)
✅ 적절하지 않은 검정을 사용하면
정규분포에서 데이터를 얻었다고 볼 수 없을 때 t검정을 사용하면 이 경우 유의수준 $ \alpha $ 를 0.05으로 설정하더라도, 제 1종 오류가 일어날 확률이 0.05가 아니게 된다. 설정한 값보다 커지는 것이 중대한 문제이다.
한편 계산되는 p값이 그 정의인 귀무가설 하에서 관찰된 값 이상으로 극단적인 값을 얻을 수 있는 확률보다 커지게 되면
제 1종 오류를 일으킬 확률이 설정한 값보다 작아진다. 이는 제 2종 오류가 일어나기 쉬운 방법이다.
그렇기 때문에 데이터 성질에 맞춰 적절한 검정 방법을 선택하는 것이 중요하는 것.
정규성 조사
모수검정에서는 각 집단의 데이터에 정규성이 있어야 한다.
- Q-Q 플롯(분위수-분위수 그림)
- 샤피로-윌크 검정
- 콜모고로프-스미르노프(K-S) 검정
귀무가설 : 모집단이 정규분포이다.
대립가설 : 모집단이 정규분포가 아니다.
p >= 0.05라면 정규성이 있고, p<0.05라면 정규성이 없다고 판단하는 경우가 많습니다.
단, 가설검정 해석에서 설명했듯 결과가 p>0.05라 귀무가설을 기각할 수 없다고 해서 귀무가설이 옳다는 증거가 되지는 않습니다.
등분산성 조사
t검정과 분산분석에는 데이터가 분산이 같은 모집단으로부터 획득되었다는 조건이 필요합니다.
- 바틀렛 검정
- 레빈 검정
귀무가설 ; 2개 모집단의 분산은 같다
대립가설 : 2개 모집단의 분산은 같지 않다
정규성 조사와 같이 p>0.05라고 해도 적극적으로 분산이 같다고 주장할 수 없다는 점 주의
비모수검정의 대푯값 비교
각 집단 데이터에 정규성이 없는 경우에는 비모수검정으로 분류되는 방법을 사용하는 것이 권장됩니다,
대표적인 방법 : 윌콕슨 순위합 검정
평균값 대신 각 데이터 값의 순위(크기 순으로 나열했을 때 몇 번째 위치인가를 나타내는 값) 에 기반하여 검정을 실시합니다.
맨 - 휘트니 U 검정
비교할 2개 집단의 분포 모양 자체가 같아야합니다.
즉, 분포는 정규분포가 아니더라도 괜찮지만, 분산이 다르다면 문제가 생길 수 있다.
윌콕슨 순위합
귀무가설 : 2개 모집단의 위치가 같다.
대립가설 : 2개 모집단의 위치가 다르다.
그 외 플리그너-폴리셀로 검정, 브루너-문첼 검정이 있다.
이 방법은 2개 모집단의 분포 형태가 같지 않을 때도 사용할 수 있는 비모수검정 방법입니다.
단, 극단적으로 분포 형태가 다른 경우에는 역시 제1종 오류가 발생할 확률이 설정한 $ \alpha $와는 달라지므로 주의해야 합니다.
분산분석(3개 집단 이상의 평균값 비교)
분산분석(ANOVA, Analysis of variance) : 3개 이상 집단의 평균값을 비교하는 방법
귀무가설 : 모든 집단의 평균이 같다($\mu_{A}=\mu_{B}=\mu_{C}$)
대립가설 : 적어도 한 쌍에는 차이가 있다.
$$ F값 = (평균적인 집단 간 변동)/(평균적인 집단 내 변동) $$
F값이 이보다 오른쪽에 있다면 유의수준 $ \alpha $ = 0.05에서 통계적으로 유의미한 집단 간 차이가 있다는 것입니다.

여기서는 전형적인 F분포 형태를 나타냈습니다만, 표본크기와 표본의 수에 따라 형태는 조금씩 다릅니다.
다중비교 검정
분산분석의 결과는 적어도 한 상에는 차이가 있다이기에 대립가설을 채택하더라도 어느 쌍에 차이가 있는지 알려면
다중비교라 불리는 방법을 사용해서 조사해야 한다.
집단이 셋 이상일 때 각 쌍의 차이를 조사하기 위해 유의수준 $ \alpha $ = 0.05에서 이표본 t검정을 반복해 실행하면, 제 1종 오류가 증가하는 문제가 생깁니다.
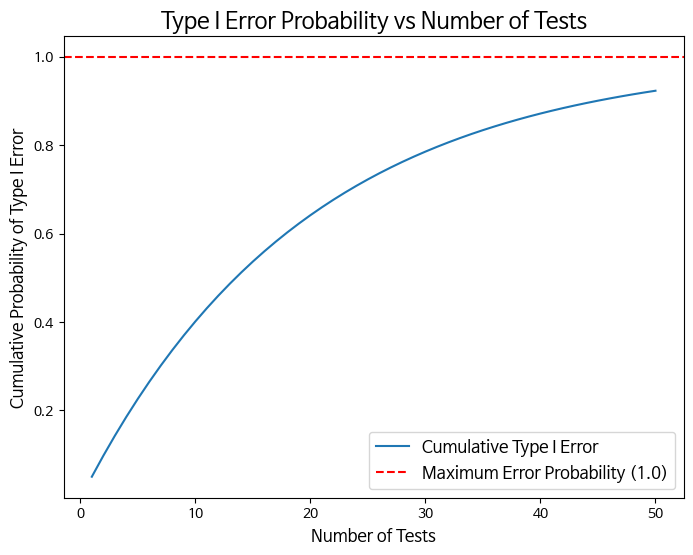
✅ 다중성 문제를 회피하고자 다중비교 검정을 사용
다중비교 검정의 기본 아이디어는 검정을 반복하는 만큼, 유의수준을 엄격한 값으로 변경하는 것
여러 가지 다중비교 방법
가장 단순한 다중비교 방법으로는 본페로니 교정이 있습니다.이는 전체에서 유의수준 $ \alpha $를 설정했을 때의 검정 반복 횟수를 k라 하고, 매 검정에서는 $\alpha$를 검정 횟수로 나눈 값 $ \alpha / k $를 기준으로 가설검증을 하는 방법
하지만, 검정력이 낮은 경향이 있어, 정말로 차이가 있을 때에 차이가 있다고 주장하기 어려울 수 있다는 단점이 있다.
그래서 보통 분산분석을 시행한 다음에는 본페로니 교정보다 우수한 방법인 튜키검정 등 다른 방법을 사용할 때가 더 많다.
- 튜키 검정 : 모든 쌍별 비교에 대해 평균의 차이를 테스트
장점 : 모든 그룹 간의 차이를 종합적으로 확인 가능
단점 : 검정의 수가 많아질수록 보수적(덜 민감) - 던넷 검정 : 대조군의 관심이 있을 때
장점 : 대조군과의 비교만 수행하기 때문에 검정력이 높음
단점 : 쌍별 비교는 불가능 - 윌리엄스 검정 : 집단 간에 순위를 매길 수 있는 경우
장점 : 단조 경향성을 효율적으로 검출 가능
단점 : 경향성이 없는 경우 사용 부적합
✅ 앞선 본페르니 검정, 튜키 검정, 던넷 검정, 윌리엄스 검정은
분산분석과 다른 원리이므로 분산분석 없이 단독으로 수행해도 문제가 없다.
3집단 이상의 비모수검정
분산분석은 모수검정으로 분류되는 방법. 그러므로 각 집단의 데이터에는 정규성이 있어야한다.
정규성이 없는 집단이 1개 이상이라면 분산분석 대신 비모수검정 방법인 크러스털-월리스 검정을 사용
비모수 다중비교 방법도 고안,
튜키 검정 : 스틸-드와스 검정
던넷 검정 : 스틸 검정
비율비교
범주형 데이터
범주형 : 동전의 앞뒤, 주사위의 눈, 좋아하는 음식
확률 : $ P $ : 앞면이 나올 확률, $ 1-P $ : 뒷면이 나올 확률
이항검정
: 하나의 범주가 확률 $ P $, 또 하나의 범주가 확률 $ 1-P $로 나타나는지 조사하는 방법
귀무가설 : 앞면이 1/2, 뒷면이 1/2 확률로 나온다(치우치지 않음)
대립가설 : 앞면이 1/2, 뒷면이 1/2 확률로 나오지 않는다(어딘가 치우침이 있음)
카이제곱검정 : 적합도 검정
이항검정은 범주가 2개일 때만 이용할 수 있습니다. 그러나 6개의 눈이 있는 주사위나 더 일반적인 이산확률분포에 이항검정의 방식을 적용하고 싶을 때가 있습니다.
귀무가설 : 모집단은 상정한 이산확률분포이다.
대립가설 : 모집단은 상정한 이산확률분포가 아니다.
적합도검정 : 얻은 출현도수(개수)가 이론적인 비율(이산확률분포)에 따라 얻어진 것인지를 조사하는 검정
| 1 | 2 | 3 | 4 | 5 | 6 | 합계 | |
| 출현도수 | 5 | 8 | 10 | 20 | 7 | 10 | 60 |
| 이론적 비율(확률) | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1 |
| 기대도수 | 10 | 10 | 10 | 10 | 10 | 10 | 60 |
$$ \chi^2 = \sum \frac{(O-E)^2}{E} = 4.33 $$
카이제곱검정 : 독립성 검정
2개의 범주형 변수 데이터는 분할표로 정리할 수 있습니다.
한쪽 변수의 범주가 바뀌었을 때 다른 쪽 변수의 범주 비율이 달라지지 않을 때, 2개 변수는 독립적이라고 말할 수 있습니다.
귀무가설 : 2개의 변수는 독립이다.
대립가설 : 2개의 변수는 독립이 아니다.
출현도수
| 수 | 암 | 합 | |
| 굴밤나무 | 14 | 9 | 23 |
| 상수리나무 | 6 | 17 | 23 |
| 합 | 20 | 26 |
기대도수
| 수 | 암 | |
| 굴밤나무 | 10 | 13 |
| 상수리나무 | 10 | 13 |
검정통계량 값은 4.33으로 p-value는 0.037으로 귀무가설 기각
대립가설 채택, 사슴벌레 암수의 비율이 나무 종류(수종)에 따라 다르다는 결론을 내릴 수 있습니다.
그 밖의 독립성검정으로는 피셔의 정확검정이 있습니다.
이는 이항검정에서 본 것처럼 초기하분포를 이용하여 모든 경우의 확률을 계산하는 방법입니다.
'Statistics' 카테고리의 다른 글
| [통계 101 x 데이터 분석] 통계 모형화 (3) | 2025.02.01 |
|---|---|
| [통계 101 x 데이터 분석] 상관과 회귀 (0) | 2025.01.28 |
| [통계 101 x 데이터 분석] 가설검증 (1) | 2025.01.22 |
| [통계 101 x 데이터 분석] 추론통계 ~ 신뢰구간 (0) | 2025.01.21 |
| [통계 101 x 데이터 분석] 통계분석의 기초 (0) | 2025.01.20 |
