| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 파이썬
- 프로젝트
- 내일배움캠프
- 내일배움
- 웹 스크랩핑
- TiL
- wil
- SQL
- 스파르타코딩
- 오블완
- 텍스트 분석
- 파이썬 완벽 가이드
- Cluster
- hackerrank
- MySQL
- 스파르타
- harkerrank
- R
- 미세먼지
- 파이썬 머신러닝 완벽 가이드
- 내일배움카드
- 파이썬 철저입문
- 회귀분석
- 티스토리챌린지
- 프로그래머스
- 파이썬 머신러닝 완벽가이드
- 중회귀모형
- 실전 데이터 분석 프로젝트
- 스파르타 코딩
- 파이썬 철저 입문
- Today
- Total
OkBublewrap
모형의 적절성 본문
가정
$$1.E(\epsilon_{i})=0, 모든 i에 대해$$
$$2.(1) V(\epsilon_{i})=\sigma ^{2}, 모든 i에 대해(등분산성)$$
$$(2) \epsilon_{i} 들은 서로 독립이다.(독립성)$$
$$(3) \epsilon_{i}는 모든 i에 대해 정규분포를 따른다(정규성)$$
잔차
$$\epsilon_{i}=y_{i}-\hat{y_{i}}$$
으로 정의된다.
1. x에 대해
2. y의 예측값 y_h에 대해
3. 시간의 순서에 따라
값을 그려봐야한다.
<최대산소흡입량 자료>
n <- 1:10
x <- c(1.54,1.74,1.32,1.50,1.46,1.35,1.53,1.71,1.27,1.50)
y <- c(132.0,135.5,127.7,131.1,130.0,127.6,129.9,138.1,126.6,131.8)
library(dplyr)
data <- cbind(n,x,y) %>% data.frame()
잔차를 구하기 위해서 y_h을 구해야한다.
lm(y~x, data) lm(formula = y ~ x, data = data)
Coefficients:
(Intercept) x
-3.84333 0.04072
으로 y_h = -3.84333 + 0.04072*x으로 회귀방정식을 얻을 수 있다.
data$y_h <- -3.84333 + 0.04072*x # data에 변수명 y_h에 회귀방정식 넣기
data$e <- y-data$y_h # data에 변수명 e에 잔차값 넣기여기까지하면 data를 보면
n x y y_h e
1 1 132.0 1.54 1.531710 0.008290
2 2 135.5 1.74 1.674230 0.065770
3 3 127.7 1.32 1.356614 -0.036614
4 4 131.1 1.50 1.495062 0.004938
5 5 130.0 1.46 1.450270 0.009730
6 6 127.6 1.35 1.352542 -0.002542
7 7 129.9 1.53 1.446198 0.083802
8 8 138.1 1.71 1.780102 -0.070102
9 9 126.6 1.27 1.311822 -0.041822
10 10 131.8 1.50 1.523566 -0.023566
으로 나온다.
1. x에 대한 잔차 그림
plot(x, data$e, xlim=c(125,140), main='RESIDUAL PLOT', ylab = 'RESIDUAL', xlab='x')
abline(h=0,col="black",lty=1) # 평행선 넣기
2. y_h에 대한 잔차 그림
plot(y, data$e, main='RESIDUAL PLOT', ylab = 'RESIDUAL', xlab='PREDICTED VALUE OF Y')
abline(h=0,col="black",lty=1)
산점도

data_model <- lm(y~x, data)
summary(data_model)Call:
lm(formula = y ~ x, data = data)
Residuals:
Min 1Q Median 3Q Max
-0.069879 -0.033144 0.001407 0.009581 0.084012
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -3.843326 0.609198 -6.309 0.000231 ***
x 0.040718 0.004648 8.761 2.26e-05 ***
예) Hooker 자료
library(readxl)
hooker <- read_excel('c:/Temp1/hooker.xlsx')
head(hooker)

온도을 x, 압력을 y로 변수명 지정
library(readxl)
hooker <- read_excel('c:/Temp1/hooker.xlsx')
head(hooker)
hooker$x <- hooker$온도
hooker$y <- hooker$압력
hooker_model <- lm(y~x, hooker)
plot(hooker_model)
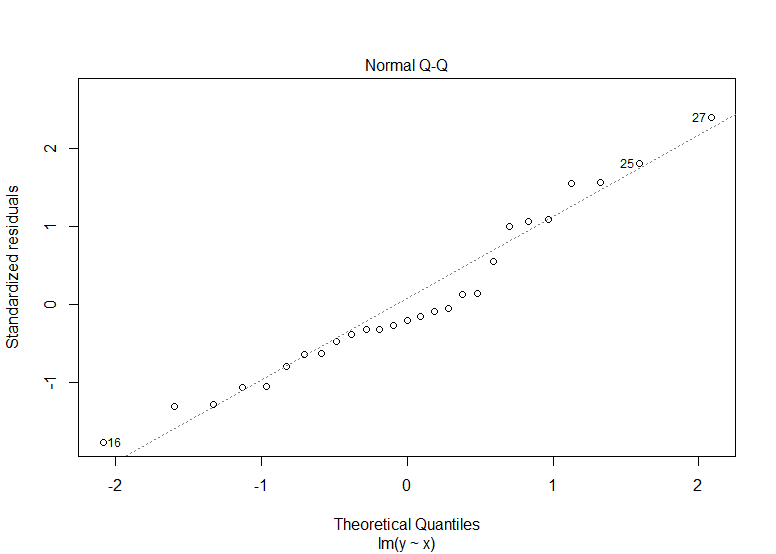

추정된 회귀식
y_h = -66.5301+0.4509*x
summary(hooker_model)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -66.530052 1.456755 -45.67 <2e-16 ***
x 0.450915 0.007531 59.88 <2e-16 ***
---
결정계수 구하기
Residual standard error: 0.3223 on 25 degrees of freedom
Multiple R-squared: 0.9931, Adjusted R-squared: 0.9928
F-statistic: 3585 on 1 and 25 DF, p-value: < 2.2e-16
결정계수 값은 0.9931로 매우 높게 나왔다.
또 F검정은 2.2e-16으로 매우 유의하게 나왔다.





